시간 복잡도
실행 시간은 하드웨어와 소프트웨어의 환경에 따라 천차 만별이다.
그렇기에 소프트웨어와 하드웨어 환경을 배제한 객관적인 지표가 필요한데 이것이 시간 복잡도 이다.
시간 복잡도는 알고리즘 수행에 연산이 몇 번 수행되는지 숫자료 표기한다.

하나 연산하는데 t 만큼 시간이 들때 계산식
case 1 = 2t
case 2 = (2n + 1) t
case 3 = (2n² + 1) t
각각의 시간 복잡도를 계산 할 수 있다.
여기서 모든 계산에 걸리는 시간을 1ms 라고 정의했을때 표를 만들 수 있다.
| 입력 값(n) | case 1(단위 : ms) | case2(단위 : ms) | case3(단위 : ms) |
| 1 | 2 | 3 | 3 |
| 10 | 2 | 21 | 201 |
| 100 | 2 | 201 | 20,001 |
| 1000 | 2 | 2,001 | 2,000,001 |
| 10000 | 2 | 20,001 | 200,000,001 |
위 표를 보면 입력 값이 적을 때는 큰 차이가 적지만, 입력 값이 커질수록 수의 차이가 커지는 것을 볼 수 있다.(성장률)
Big - O 표기법
Big - O 표기법은 위 표에서 2(10000²) + 1 의 +1 과 같이 영향이 적어 중요하지 않은 부분을 제외하고 표기하는 표기방법으로 점근적 표기법을 사용한다.
그래서 위 계산식을 Big - O 표기법으로 바꾸면 O(1), O(n), O(n²) 으로 표기하게 된다.
여기서 Big - O 표기법을 이용해 계산 속도의 순서를 나타냈다.
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2ⁿ) < O(n!)
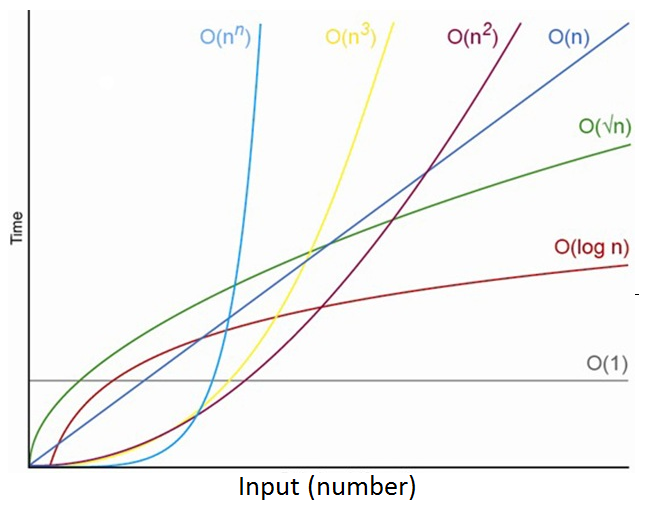
여기서 유의할 점은 알고리즘의 전체적인 속도 차이가 있다고 해도 값에 따라 속도가 다를 수 있는데
위 그래프의 n 과 n² 를 보면 O(n) < O(n²) 지만 n이 n² 를 넘기는건 중반 이후 부터다.
공간 복잡도
알고리즘의 성능을 따지는 요소는 실행 시간 외 요소도 존재한다.
공간 복잡도는 알고리즘을 사용하는데 필요한 자원 공간의 양 혹은 크기이다.
공간 복잡도 함수는 총 공간 요구 = 고정 공간 요구 + 가변 공간 요구
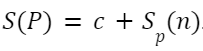
고정 공간 : 입력과 출력의 횟수나 크기와 관계 없는 공간
가변 공간 : 문제를 해결하기 위해 요구되는 추가 공간(동적으로 필요한 공간)
팩토리얼을 사용한 공간 복잡도
두 팩토리얼 구현 방식을 보며 공간복잡도를 비교해 보자.
int factorial(int n)
{
if(n > 1) return n * factorial(n - 1);
else return 1;
}n이 1 이하일 때까지 함수가 재귀적으로 호출되어 스택에 n부터 1까지 쌓이게 되므로 공간 복잡도는 O(n)이 된다.
int factorial(int n)
{
int fac = 1;
for(int i = 1; i <= n; i++)
{
fac = fac * i;
}
return fac;
}n 값이 뭐가 나오든 스택에는 n , i , fac 만 저장되기에 공간 복잡도는 O(1)이 된다.
시간복잡도 와 공간복잡도
가장 효율적인 알고리즘은 실행시간이 적고 자원을 적게 소모하는 것이다.
하지만, 시간과 공간은 반비례적인 경향이 있어 보통 효율을 볼 때 시간복잡도를 보기에 시간복잡도를 위해 공간복잡도를 희생하는 경우가 많다.
'코딩 > 자료구조' 카테고리의 다른 글
| [자료구조] 스택(Stack) (0) | 2022.07.04 |
|---|---|
| [자료구조] 연결 리스트 (0) | 2022.06.20 |
| [자료구조] STL (0) | 2022.06.07 |
| 자료구조 (0) | 2022.06.07 |
| [자료구조] 특수화 (0) | 2022.05.09 |